Persamaan dan pertidaksamaan irasional
Persamaan Dan Pertidaksamaan Rasional
Persamaan irasional (irrational equation) adalah persamaan yang melibatkan variabel dalam tanda akar. Lima contoh berikut semuanya merupakan persamaan irasional. Sedangkan ertidaksamaan irasional atau pertidaksamaan bentuk akar adalah pertidaksamaan yang memuat fungsi irasional atau bentuk akar.
Contoh soal Persamaan Irasional:
Selesaikanlah Persamaan irasional,

Tentukan terlebih dahulu prasyarat, yaitu:

Contoh 2:




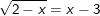 , [Solusi]Tentukan terlebih dahulu prasyarat :
, [Solusi]Tentukan terlebih dahulu prasyarat : Selanjutnya selesaikan:
Selanjutnya selesaikan: Jadi, persamaan rasional,
Jadi, persamaan rasional, 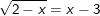 tidak mempunyai solusi.
tidak mempunyai solusi. Tentukan himpunan penyelesaian dari,




Jawab.
Contoh soal persamaan irasional tersebut dapat dihitung dengan metode seperti di bawah ini:
4x + 8 ≥ 0 → x ≥ -2 . . . (1)
x + 2 ≥ 0 → x ≥ -2 . . . (2)
Sehingga diperoleh x ≥ -2 dari persamaan (1) dan (2) ini
Cara menghitung persamaan irasional selanjutnya dengan mengkuadratkan kedua ruasnya. Maka hasilnya: 4x + 8 = x² + 4x + 4
x² – 4 = 0
x = 2
Contoh soal persamaan irasional di atas dapat digambarkan dalam bentuk grafik seperti di bawah ini:
Berdasarkan grafik di atas dapat kita ketahui bahwa kedua titik tadi saling berpotongan seperti titik x = 2 (yang ditunjukkan dengan garis tebal) dan x = -2 (yang ditunjukkan dengan garis putus putus).
Contoh 6:
Tentukan persamaan irasional dari ?
Jawab.
Contoh soal persamaan irasional tersebut dapat dihitung dengan cara mengkuadratkan kedua ruasnya. Maka hasilnya akan menjadi seperti berikut:4x + 8 = 0
4x = -8
x = -2
Cara menghitung persamaan irasional selanjutnya yaitu memenuhi syarat akarnya seperti di bawah ini:
4x + 8 ≥ 0 → x ≥ -2
Syarat x ≥ -2 terpenuhi karena nilai x = -2, sehingga penyelesaian ini dapat diterima.
Jadi penyelesaian persamaan irasional tersebut ialah x = -2.
Contoh Soal Pertidaksamaan Irasional:
1. Tentukanlah himpunan penyelesaian atas pertidaksamaan dibawah ini :
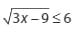
Jawaban :
Bentuk tersebut dapat terpenuhi jika diperoleh :
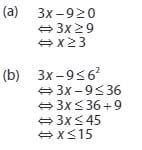
Penyelesaian himpunan pertidaksamaan irasional ini merupakan suatu irisan dari (a) dan (b). Sehingga diperoleh hasil :

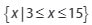
Berdasarkan penjelasan diatas dapat disimpulkan jika hasil himpunan penyelesaian atas pertidaksamaan tersebut ialah disamping ini
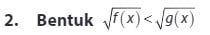
Bentuk ini dapat terpenuhi jika :
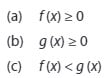
” Sesuai tanda ketidaksamaan yang diberikan”.
Penyelesaian : Merupakan irisan dari (a), (b), dan (c)
2. Tentukanlah himpunan penyelesaian atas pertidaksamaan dibawah ini :
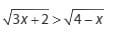
Jawaban :
Bentuk tersebut dapat dipenuhi jika :

Penyelesaian pertidaksamaan irasional adalah suatu irisan dari (a), (b), dan (c). Sehingga diperoleh hasil :
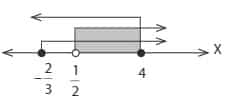
Berdasarkan hasil yang diperoleh diatas dapat disimpulkan hasil dari pertidaksamaan tersebut dibawah ini
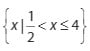
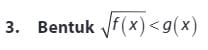
Bentuk ini dapat terpenuhi jika :

Penyelesaian : Merupakan irisan dari (a), (b), dan (c).
3. Tentukanlah himpunan penyelesaian dari pertidaksamaan dibawah ini
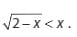
Jawaban :
Bentuk tersebut dapat dipenuhi jika

Titik pembuat nol adalah x = -2, x =1.
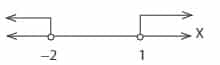
Penyelesaian : x < -2 dan x > 1
Penyelesaian pertidaksamaan irsional merupakan irisan dari (a), (b), dan (c). Sehingga diperoleh :
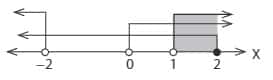
4. Hasil penyelesaian himpunan pertidaksamaan adalah dibawah ini
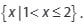
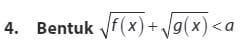
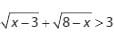
Himpunan penyelesaian dari pertidaksamaan
adalah
A. x > 7
B. 4 < x < 7
C. x < 4
D. -4 < x < 7
E. 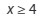
Jawaban :
Bentuk tersebut dapat terpenuhi jika :

Titik pembuat nol x = 4, dan x = 7 adalah sebagai berikut :

Penyelesaian : 4 < x < 7
Penyelesaian himpunan pertidaksamaan irasional merupakan irisan dari (a), (b), dan (c). Sehingga dapat diperoleh sebagai berikut

Jadi dapat disimpulkan himpunan dari penyelesaian pertidaksamaan diatas adalah 4 < x < 7.
Daftar Pustaka:
https://soulmath4u.blogspot.com/2013/10/persamaan-irasional.html
http://www.antotunggal.com/2021/09/pembahasan-contoh-soal-persamaan-irasional.html
https://rumusrumus.com/materi-pertidaksamaan-irasional/




Komentar
Posting Komentar